The Good, the Not So Bad, and the Full General

Just like shopping for a new refrigerator, picking a linear equation solver in OpenSees (via the system command) can lead to paralysis of choice. And while you can consult Consumer Reports for the pros and cons of refrigerators A, B, and C, the only way to figure out the pros and cons of OpenSees solvers is to run your own test cases.

The solid bar model shown in this post is as good a test case as any other. Using successively refined mesh sizes of c=t/1.5, t/2, t/2.5, and t/3, with 585, 1200, 2304, 3894 equations, respectively, should give a good idea how well the various linear equation solvers perform. The model sizes are not very large because I want my crappy laptop to complete the analyses in reasonable time.

A static analysis of the bar model is performed for an increasing load (not important) over 10 pseudo time steps. I used more than one time step to cut down on variance in short run times. All things being equal, differences in run-time can be attributed to the equation solver.

The compute times reported in the plots below are wall times for all parts of the OpenSees analysis, not just the CPU time for only the solver.

---

It’s fairly well known that equation numbering can have a significant effect on linear equation solvers. But because the FullGeneral solver is so slow, all other solvers appear to perform equally well when using the RCM equation numberer.

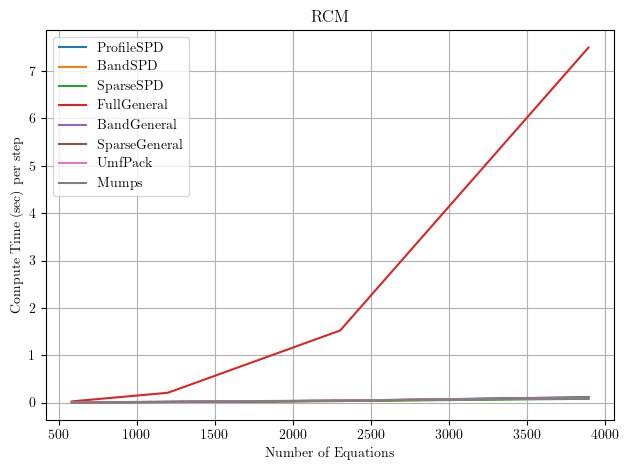
For reference, the stiffness matrix topology for the c=t/2 mesh size is shown in this post for the Plain, AMD, and RCM equation numberers available in OpenSees. Fortunately, RCM is the default option for the numberer command.

Changing the numberer to AMD, which leads to a large matrix bandwidth, the solvers start to sort themselves out.

Same deal with the Plain numberer.

It’s obvious from the foregoing results that the equation numberer affects the run-time significantly for some solvers, but has no effect on other solvers, indicating some solvers override OpenSees and use their own internal equation numbering.

We can get a better idea of what’s happening with equation numbering if we drill down to each solver.

ProfileSPD

The ProfileSPD solver uses profile matrix storage and assumes the matrix is symmetric and positive definite. This is the default option for the system command in OpenSees, I believe because Frank wrote the solver himself.

Assessment: Not so bad

BandSPD

The BandSPD solver is designed for symmetric, positive definite matrices and assumes banded matrix storage. For this model, the AMD numberer gives a slightly higher matrix bandwidth than the Plain numberer.

Assessment: Not so bad

SparseSPD

The SparseSPD solver assumes sparse storage of symmetric, positive definite matrices. As far as I know, this solver is one of the lesser used solvers in OpenSees. But perhaps the solver should be used a little more often. Note that this solver is not affected by the equation numbering provided by OpenSees.

Assessment: Good

FullGeneral

The FullGeneral solver assumes full matrix storage for general matrices. The equation numberer does not matter.

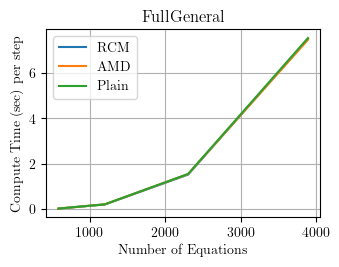
Assessment: The full general

BandGeneral

The BandGeneral solver assumes banded matrix storage for general matrices. Again, the AMD numberer leads to high bandwidth for this model.

Assessment: Not so bad

SparseGeneral

The SparseGeneral solver assumes sparse storage for general matrices. I would not expect the equation numberer to matter for sparse storage, but it does for some reason.

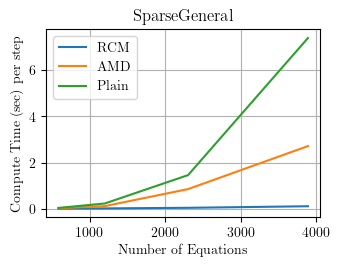
UPDATE (November 15, 2024): Based on input from Gustavo (see comments below), Frank updated the permSpec variable to be non-zero (commit 24147d3). Now the SparseGeneral solver gives the expected results.

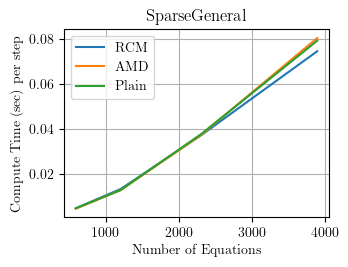
Assessment: Not so bad Good

UmfPack

UmfPack is a sparse matrix solver developed for general matrices. The solver is impervious to the OpenSees equation numbering.

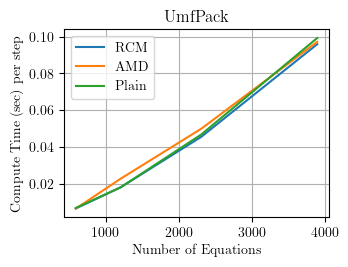
Assessment: Good

Mumps

Mumps is another general, sparse matrix solver, also indifferent to the equation numbering passed in by OpenSees.

Assessment: Good

---

That’s a quick run-down of the good, the bad, and the ugly among linear equation solvers in OpenSees. The SparseSPD and SparseGeneral solvers appear to be faster than UmfPack and Mumps for this model and analysis, but just like refrigerators, every solver has its pros and cons.