Not All at Once

I’ve been working on a project where we use OpenSees to analyze structural models for several load cases. We only care if the models can support the full load, not so much how they get to the full load.

We apply all the load in one step with load control and Newton-Raphson. If that succeeds, we move on to the next load case. But if that analysis fails, we fall back to multiple load steps to see if we can converge to the full load in increments. If that doesn’t converge, we’ll get an idea of the load level where the model runs into problems, then move on to the next load case.

For some load cases on specific models, Newton-Raphson would converge in one step to 100% load. With the analysis sequence described above, everything seemed fine because plan A succeeded. However, the results were strange and counter-intuitive.

Maybe it was the convergence test, so we checked the norms from the one step analysis. The norms of the displacement increment and residual were on the order of 10^-7 and 10^-6, respectively. The model had stopped moving and was in equilibrium.

To get a better idea of what was going on, we then ran these strange cases with multiple load steps. Surprisingly, the analysis failed to converge beyond 80% of the full load. That’s right, convergence with 100% of the load applied in one step, but non-convergence when taking multiple steps to reach the full load.

This is contrary to everything I thought I knew about Newton-Raphson and load control.

Plotting the load-displacement response revealed the issue. With one load step, the model displaced in the opposite direction from the solution with multiple load steps.

Could the one step solution have jumped over a limit point? To answer this question, we plotted the load-displacement relationship for loads greater than 100%. Sure enough, there were two solution paths and a limit point between 80% and 100% of the full load.

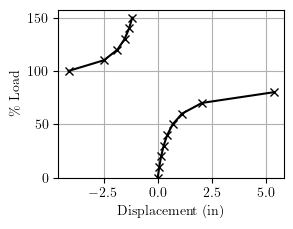
And these models are of structures you see every day, not the academic problems you see in textbooks.