Ordinary Eigenvalues

Nonlinear Analysis 2 Minutes

There are three applications of eigenvalue analysis in structural engineering. Vibration analysis and buckling analysis involve generalized eigenvalue analysis. OpenSees does vibration eigenvalue analysis pretty well, but does not perform buckling eigenvalue analysis–although you might be able to fake the geometric stiffness matrix for simple frame models.

The third application of eigenvalue analysis is ordinary (non-generalized) spectral decomposition of the material stiffness matrix, {\bf K}{\bf x}=\lambda {\bf x}, which tells you how a structural model wants to deform. The lower the eigenvalue, \lambda, the easier it is for the model to deform in the shape of the associated eigenvector, {\bf x}. If you get a zero eigenvalue, there is a rigid body displacement mode in your model.

There are two approaches to finding the spectral decomposition of the stiffness matrix in OpenSees. The first approach is to use the default generalized eigenvalue solver in OpenSees after making the mass matrix equal to the identity matrix.

#
# Define your model
#

NDF = ops.getNDF()[0]
ones = [1]*NDF
for nd in ops.getNodeTags():
   ops.mass(nd,*ones) # 1,1,...,1

Nmodes = 2 ;# Or whatever
lam = ops.eigen(Nmodes)

The second approach is to use the 'symmBandLapack' option with the eigen command. This is not a generalized eigenvalue solver so you don’t have to worry about the “mass” matrix.

#
# Define your model
#

Nmodes = 2 ;# Or whatever
lam = ops.eigen('standard','symmBandLapack',Nmodes)

The 'standard' input is not entirely necessary. It’s there to make sure you’re aware the eigen command is not going to solve a generalized eigenvalue problem, like clicking “OK” before deleting a file.

There’s a third approach: get the stiffness matrix from printA, then use an eigenvalue solver in Python, e.g., scipy.linalg.eig. This is fine for getting eigenvalues, but you’ll have a hard time mapping the eigenvectors back to the structural model.

Consider a simple beam with two DOFs–the two end rotations. The stiffness matrix contains the basic stiffness coefficients 4EI/L and 2EI/L.

The lowest eigenpair (2EI/L, [1,-1]) corresponds to symmetric bending, indicating this is the easiest way for the beam to flex while the highest eigenpair (6EI/L, [1,1]) corresponds to the more difficult case of anti-symmetric bending. The spectral decomposition tells us that, in the absence of member loads, the flexure of a simple beam is always some combination of symmetric and anti-symmetric bending.

After defining the model and calling the eigen command, you can use the nodeEigenvector command to see the components of the eigenvectors at each node.

import openseespy.opensees as ops

L = 120
E = 29000
A = 12
I = 800

ops.wipe()
ops.model('basic','-ndm',2,'-ndf',3)

ops.node(1,0,0); ops.fix(1,1,1,0)
ops.node(2,L,0); ops.fix(2,1,1,0)

ops.geomTransf('Linear',1)
ops.element('elasticBeamColumn',1,1,2,A,E,I,1)
 
lam = ops.eigen('-standard','-symmBandLapack',2)
 
print('Computed eigenvalues:',lam)
print('Expected eigenvalues:',2*E*I/L,6*E*I/L)

print('Eigenvector 1')
print(ops.nodeEigenvector(1,1,3),ops.nodeEigenvector(2,1,3)) # node, mode, dof
print('Eigenvector 2')
print(ops.nodeEigenvector(1,2,3),ops.nodeEigenvector(2,2,3))

The symmBandLapack eigenvalue solver gives the expected results.

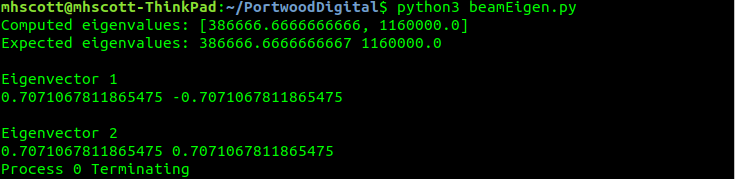
Note that the solver normalized the eigenvectors to have unit length.

Unknown's avatar

Published by Michael H. Scott

I have been involved in the development, maintenance, and growth of OpenSees since its early days. I am interested in learning Python and improving my academic writing.

Published

7 thoughts on “Ordinary Eigenvalues”

  1. Pingback: Eigenvalues of the Stiffness Matrix – Portwood Digital

  2. Hi, professor!
    I have a question about eigen command.

    In this post example, when symmBandLapack and fullGenLapack is used, the result is different respectively. So Which solver do we choose when we do eigenanalysis?

    Like

    Reply

  3. Greetings Prof. Scott,

    This topic is not discussed quite often in the literature, which leaves me with a couple of questions.

    1. How is OpenSees able to map the eigenvectors to the model?
    2. Is there any sources that I can use to learn more about the ordinary eigenvalue analysis in structural models? (So far, every book I’ve read refers to the dynamic and buckling analyses.)

    Thank you again for these great posts!

    Like

    Reply

    1. I’m not sure I understand your first question, but OpenSees maps eigenvectors to nodes via equation numbers.
      For your second question, I believe ordinary eigenvalue analysis of structural models an interesting academic exercise, but not useful in practice. I saw this paper recently: https://link.springer.com/article/10.1007/s11831-024-10082-x
      I do not know if this paper is worthwhile, but am leaving it here for my own future reference.
      Also available on ResearchGate: https://www.researchgate.net/publication/381908806_Static_Modal_Analysis_A_Review_of_Static_Structural_Analysis_Methods_Through_a_New_Modal_Paradigm

      Like

      Reply

      1. Thank you Professor!

        Regarding the first question, I was referring to this paragraph:

        There’s a third approach: get the stiffness matrix from printA, then use an eigenvalue solver in Python, e.g., scipy.linalg.eig. This is fine for getting eigenvalues, but you’ll have a hard time mapping the eigenvectors back to the structural model.

        To clarify, my question have should been: “Why is it that scipy will give me a hard time mapping the eigenvectors, when compared to the OpenSees implementation?”

        As to the second question, it may not be all that significant, but it sure is interesting. After some more digging, I was able to find in K-J Bathe’s “Finite Element Procedures” some more information on the topic.

        Once again Professor, thank you kindly for your responses!

        Like

Leave a reply to JAEMIN Cancel reply

This site uses Akismet to reduce spam. Learn how your comment data is processed.