Partial-Span Uniform Loads

Although no one is going to use OpenSees to compute tributary loads for one-way floor systems, it’s still satisfying to analyze the resulting beam models.

A common example is a beam that frames around one side of a floor opening. On the side of the beam with no opening, tributary area calculations produce a uniform distributed load (UDL) over the entire span, while on the side with an opening, the calculations lead to a uniform load applied over only part of the span. A free body diagram of such a beam would look something like below.

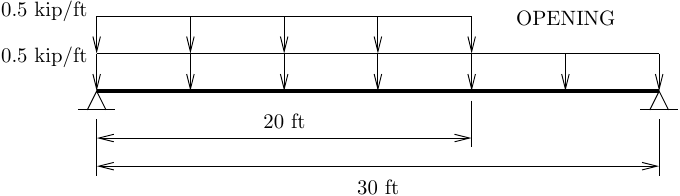
The beam is statically determinate, so we can use hand calculations to solve for the reactions and draw the bending moment diagram. But can we get OpenSees to match these hand calculations?

We can account for the stepped uniform load using two element loads: one across the entire span and the other along only a portion of the span. Currently, only the forceBeamColumn element handles uniform loads over a portion of the element length. Sure, we could just as easily subdivide the beam into two elements, each with a full-length UDL, but that’s not much fun.

import openseespy.opensees as ops
from math import isclose

kip = 1.0
ft = 1.0

inch = ft/12
ksi = kip/inch**2

L = 30*ft
w = 0.5*kip/ft

E = 29000*ksi
# W21x44
A = 13*inch**2
I = 849*inch**4

ops.wipe()
ops.model('basic','-ndm',2,'-ndf',3)

ops.node(1,0,0); ops.fix(1,1,1,0)
ops.node(2,L,0); ops.fix(2,0,1,0)

ops.section('Elastic',1,E,A,I)
Np = 10 # Many integration points to resolve internal bending moment
ops.beamIntegration('Lobatto',1,1,Np)

ops.geomTransf('Linear',1)

ops.element('forceBeamColumn',1,1,2,1,1)

ops.timeSeries('Constant',1)
ops.pattern('Plain',1,1)
# One full-span and one partial-span uniform distributed load
ops.eleLoad('-ele',1,'-type','beamUniform',-w)
ops.eleLoad('-ele',1,'-type','beamUniform',-w,0,0,2.0/3)

ops.analysis('Static','-noWarnings')
ops.analyze(1)

ops.reactions()
R1 = ops.nodeReaction(1,2)
assert isclose(R1,w*L/2 + 4*w*L/9) # full-span + partial-span reaction

The computed and exact bending moment diagrams for the beam are shown below. As expected, the bending moments are asymmetric due to the partial-span UDL.

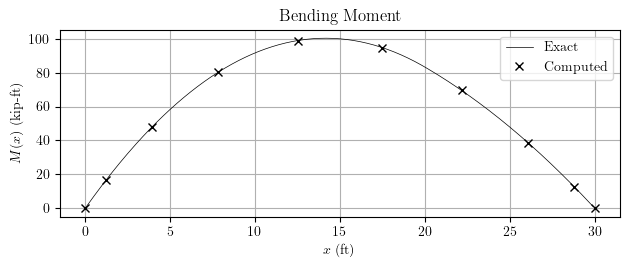
Instead of stacking a partial-span and a full-span load, we can also split the stepped loading into two partial-span UDLs.

# Remove and re-define the load pattern
ops.remove('loadPattern',1)
ops.pattern('Plain',1,1)
# Two partial-span uniform distributed loads
ops.eleLoad('-ele',1,'-type','beamUniform',-2*w,0,0,2.0/3)
ops.eleLoad('-ele',1,'-type','beamUniform',-w,0,2.0/3,1)

ops.analyze(1)
ops.reactions()

Verify for yourself that the two loading definitions give the same reactions and internal bending moments.