Torsional Buckling

From time to time, I dabble with the OpenSees warping elements developed at the University of Sydney in 2011 for doubly symmetric sections, then in 2016 for open sections.

Since my last foray into warping, I’ve taken the nonlinear displacement-based formulation from “it compiles” to “it works”. Some other ancillary changes to the warping fiber section were required, but that’s a detail for another day.

Torsional buckling of a W-shape column is one of the examples presented by the Sydney group. The column is subjected to an increasing axial load, P, after introducing twist by imposing a small torsional moment (485 N-mm) at mid-height. The torsional moment is held constant as the axial load increases.

The ends of the column are restrained against transverse motion and twist, but allowed to warp. Vertical displacement is restrained at column mid-height. The column is discretized into multiple elements with corotational transformation (the only option for the warping elements) and the section is discretized into 32 fibers through the web and 32 fibers in each flange with only one fiber through the thickness of each section element. The material response is linear-elastic.

import openseespy.opensees as ops

# Units = N,mm
d = 100
tw = 3
bf = 75
tf = 3
J = 2223

E = 2.0e5
v = 0.3
G = 0.5*E/(1+v)

L = 6000
Nele = 4
dL = L/Nele

ops.wipe()
ops.model('basic','-ndm',3,'-ndf',7)

ops.uniaxialMaterial('Elastic',1,E)
ops.section('WFSection2d',1,1,d,tw,bf,tf,32,1,32,1,'-warping','-GJ',G*J)
Np = 3
ops.beamIntegration('Legendre',1,1,Np)

ops.geomTransf('Corotational',1,0,0,1)

ops.node(0,0,0,0)
ops.fix(0, 1,0,1,0,1,0,0)
for i in range(Nele):
    ops.node(i+1,0,(i+1)*dL,0)
    ops.element('dispBeamColumnWarping',i+1,i,i+1,1,1)
ops.fix(Nele, 1,0,1,0,1,0,0)

# Vertical restraint at middle node
ops.fix(Nele//2, 0,1,0,0,0,0,0)

# Apply torsional moment
ops.timeSeries('Constant',1)
ops.pattern('Plain',1,1)
ops.load(Nele//2, 0,0,0,0,485,0,0)

ops.system('UmfPack')
ops.integrator('LoadControl',0)
ops.test('NormDispIncr',1e-6,10,0)
ops.algorithm('Newton')

ops.analysis('Static','-noWarnings')
ops.analyze(1)

# Axial load
ops.timeSeries('Linear',2)
ops.pattern('Plain',2,2)
ops.load(0, 0,1,0,0,0,0,0)
ops.load(Nele, 0,-1,0,0,0,0,0)

Pmax = 200e3
Nsteps = 1000
dP = Pmax/Nsteps
ops.integrator('LoadControl',dP)

ops.analyze(Nsteps)

The computed relationship between axial load and twist angle at mid-height of the column is shown below for increasing number of elements.

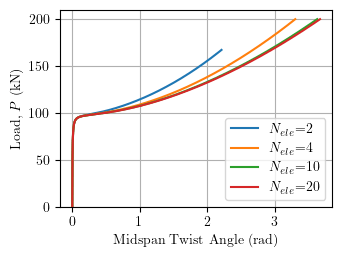
As described in the 2016 report, the theoretical buckling load is P=98 kN. The post-buckling response converges with 10 elements and matches an Abaqus analysis with 3600 S8R shell elements (also described in the report). The final twist angle is 3.67 radians, or about 210 degrees!