Legend has it that some published research results based on nonlinear dynamic analysis–incremental dynamic analyses, seismic fragility curves, Monte Carlo simulations, etc.–considered a non-convergent OpenSees model to indicate structural collapse or failure.
Let’s think about this for a minute.
Here is the displacement response in two orthogonal directions at the top of a nearly 50 m tall structural model subjected to two components of earthquake ground motion. The analysis fails to converge at about 11 seconds into a 60 second simulation.
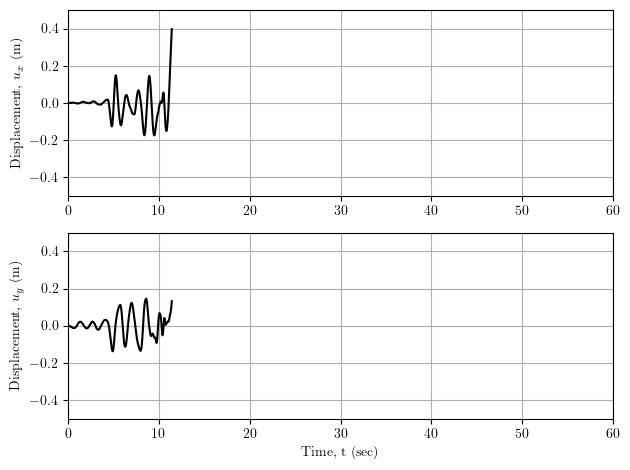
Has this structural model collapsed? At 0.4 m, or less than 1% drift, probably not.
If the performance criteria is that the displacement remain under 0.5 m, did this structural model perform acceptably? Maybe, but it sure looks like the displacement is headed to 0.5 m in a hurry.
Oops, I forgot to define damping! Rayleigh–1.5% at periods 0.5 sec and 5.0 sec.
Let’s run that again.
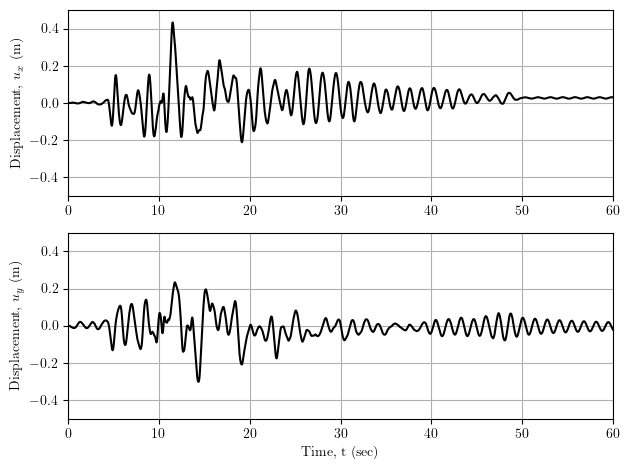
Much better. There’s some residual displacement, but no collapse, no failure.
For this model, a small amount of damping makes a difference, killing off the higher modes of response; however, there’s many other ways to remedy non-convergence, e.g., by using variable time steps and algorithm switching. But first, check your model.

Dear Professor Scott
Thank you for your post. You discussed the nuances of non- convergence topics. Your observation of the issues and narrative on them is awesome.
LikeLiked by 1 person
Thanks Prof Scott for highlighting this important issue.
The same ‘belief’ of non-convergence as a sign of failure is also popular among Geotechnical FEA colleagues, particularly while analysing static slope stability using the Strength Reduction Method. May be, the same was true or a meaningful conclusion during the days of FEA implemented in Computers of late ’80s and early ’90s. However, for today’s sophisticated non-linear solvers (both for commercial and more so for OSS like OpenSees, Code-aster, RealESSI etc.), coupled with decent computing powers of today’s common PCs/laptops (let alone be the cloud computing platforms), such a conclusion is no longer valid. For example, in a slope analysis problem, instead of relying on non-convergence to identify failure, one needs to monitor the (static) load-settlement response and also many a times the shear strain contours showing failure bands/surfaces within the slope. In a nutshell, your observations are true, not only specifically for OpenSees or Dynamic Analysis, but also for a wide range of FEA applications.
LikeLiked by 1 person
Can no convergence be solved with using more digits in calculations. Maybe you can use in c++ bignum library – arbitrary precision arithmetic and check whether using more digits in a calculation can improve convergence.
LikeLiked by 1 person
I doubt that will make a difference. The non-convergence is almost always due to modeling issues, not numerical calculation/round off issues.
LikeLike
Sir, I think it may. In example Fortran has single precision and double precision for variables. In example Ls-Dyna (Livermore Software-Now Ansys purchased) has two versions, SNG (Single Precision) and DBL (Double Precision) (https://www.lstc.com/download/ls-dyna_(win)).
LikeLike
OpenSees uses all double precision variables, at least on the C++ side. If you think it may make a difference, then come up with a MWE in OpenSees that demonstrates the issue.
LikeLike
I cannot implement it to openSees, maybe I can use my own matlab codes. I do not know c++ very well
LikeLiked by 1 person
If you’re going to be precise, you’d better be accurate!!!!
LikeLiked by 2 people
Could you please send me your email address, so I can send you matlab files. In 32 digits, calculations do not converge, but in 64 it converges. A very simple example.
LikeLiked by 1 person
How about you send me a detailed description of the FE model and I’ll see if I can reproduce the non-convergence in OpenSees?
LikeLiked by 1 person
Ok, I am sending
LikeLiked by 1 person
As you know you are using Newton-Raphson like algorithm, since it is nonlinear. You should remember from static analysis that, load control fails after buckling/limit load etc. since, you cannot pass the limit point. Since also there is Newton-Raphson in time history, if you look carefully to what we do, there is a load control like mechanism. In general, if you decrease the time step, you can have convergence (not always) since it is like dividing the dynamic analysis into smaller load control like steps. As you should experience, in general nonconvergence exists while large amount of acceleration values passed. We think (with my son, N.S.), decreasing time step is similar to decreasing load control step size. So, where we experience high jumps at earthquake accelerations, we can divide into more time steps at those time intervals by looking at the earthquake record. So, the algorithm can be adaptive/allows changes in time step size. I guess, you may not always get convergence since although you get results for points passing the limit point, you may still observe fictitious limit point. Stiffness limit point is one thing, damping and mass effects make it pass the limit point at stiffness, however, as I tried to explain, you may not always pass the resulting fictitious limit point…
LikeLike
maybe displacement control, or arc-length like things may help convergence. I do not know how to make them work for nonlinear direct integration time history analysis, however, if time step is like load control, maybe there may exist a way to implement displacement control or arc-length control like mechanisms at nonlinear dynamic analysis. I do not know exactly how displacement control works. 🙂
LikeLike